[Kotlin] 백준 1002 : 터렛
문제 링크
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
문제 해설
2개의 점과 각 점에서 류재명까지의 거리가 주어지고 이를 이용하여 류재명이 있을 수 있는 좌표의 수를 구하는 문제이다. 문제를 잘 보면 조규현과 백승환의 좌표를 각각 A, B라고 했을 때, A가 중심이고 반지름이 r1인 원과 B가 중심이고 반지름이 r2인 원이 만나는 점의 개수를 구하는 문제라는 것을 알 수 있다.
이제 각 경우에 대해 그림을 보면서 생각해보자.
1. 두 원의 접점이 무수히 많은 경우

두 원의 중심과 반지름의 길이가 모두 같은 경우는 곧 두 원이 일치하는 경우이다. 문제의 입력상으론 x1 = x2, y1 = y2, r1 = r2인 경우이다. 이 경우에는 류재명이 있을 수 있는 위치가 무한대이므로 -1을 출력해야 한다.
2023.06.22 추가내용
여기서 r1 = r2 = 0인 경우도 생각해봐야 한다. 두 원의 중심이 같으면서 두 원의 반지름의 길이가 모두 0이면 결국 하나의 점(중심)에서만 만나게 된다. 따라서, r1 = r2 = 0 인 경우는 제외해야 한다.
2. 두 원의 접점이 존재하지 않는 경우

위 그림의 (1) 처럼 두 원의 중심이 다르고, 두 원의 반지름의 차이가 두 점 사이의 거리보다 긴 경우, (2) 처럼 두 원의 중심은 같으나 반지름의 길이가 다른 경우, (3) 처럼 두 원의 반지름의 합계가 두 점 사이의 거리보다 짧은 경우에는 류재명이 있을 수 있는 위치가 존재하지 않는다. 이 경우에는 0을 출력해야 한다.
3. 두 원이 하나의 점에서 만나는 경우

위 그림의 (1) 처럼 한 원의 내부에 다른 원이 존재 하면서 두 점 사이의 거리가 반지름의 차이와 일치하는 경우, 즉 작은 원의 반지름과 두 점 사이의 거리를 합한 값이 큰 원의 반지름 길이와 일치하는 경우와 두 점 사이의 거리가 두 원의 반지름 합계와 일치하는 경우에는 류재명이 있을 수 있는 위치가 한 점 뿐이므로 1을 출력해야 한다.
4. 두 원이 2개의 점에서 만나는 경우
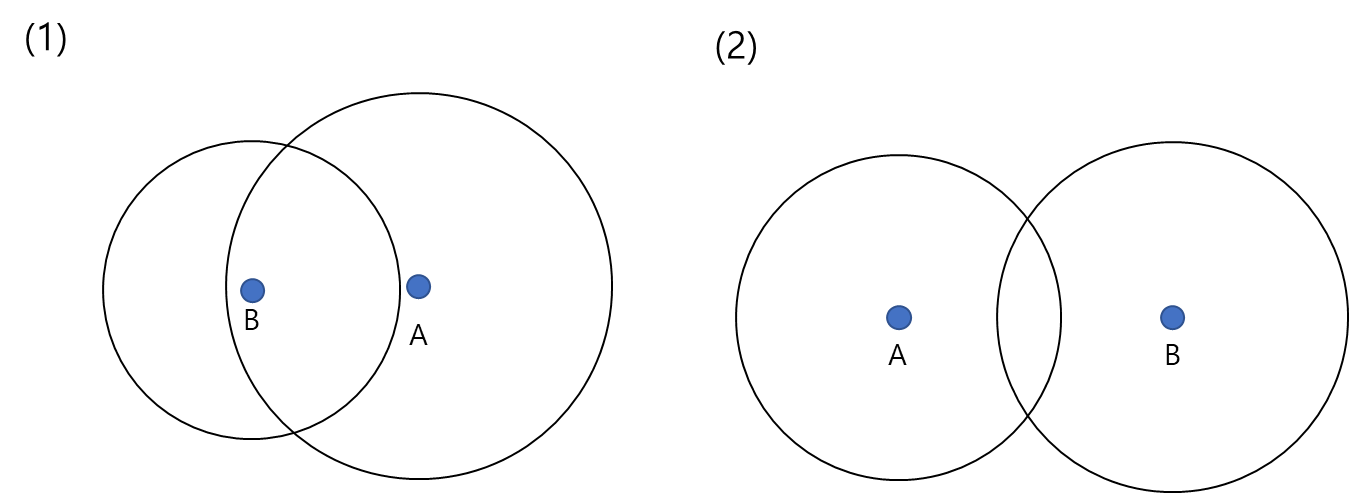
나머지의 경우는 위 그림의 (1) 처럼 두 원의 반지름 길이의 차이가 두 점 사이의 거리보다 작은 경우, 즉 작은 원의 반지름 길이와 두 점 사이의 거리를 합한 값이 큰 원의 반지름 길이보다 크거나 두 점 사이의 거리가 두 원의 반지름 합계보다 작은 경우가 남는다. 이 경우에는 그냥 else로 처리해줄 수 있다.
Code
import java.util.StringTokenizer
fun main() = with(System.`in`.bufferedReader()) {
val bw = System.out.bufferedWriter()
val n = readLine().toInt()
repeat(n) {
val input = StringTokenizer(readLine()).run { LongArray(6) { nextToken().toLong() } }
bw.write("${calc(input)}\n")
}
bw.close()
}
private fun calc(l: LongArray): Int {
val distance = (l[3] - l[0]).pow() + (l[4] - l[1]).pow()
val result = when {
distance == 0L && l[2] == l[5] && l[2] != 0L -> -1
distance > (l[2] + l[5]).pow() || distance < (l[2] - l[5]).pow() || (distance == 0L && l[2] != l[5]) -> 0
distance == (l[2] + l[5]).pow() || distance == (l[2] - l[5]).pow() -> 1
else -> 2
}
return result
}
private fun Long.pow() = this * this