[Kotlin] 백준 14943 : 벼룩 시장
문제 링크
14943번: 벼룩 시장
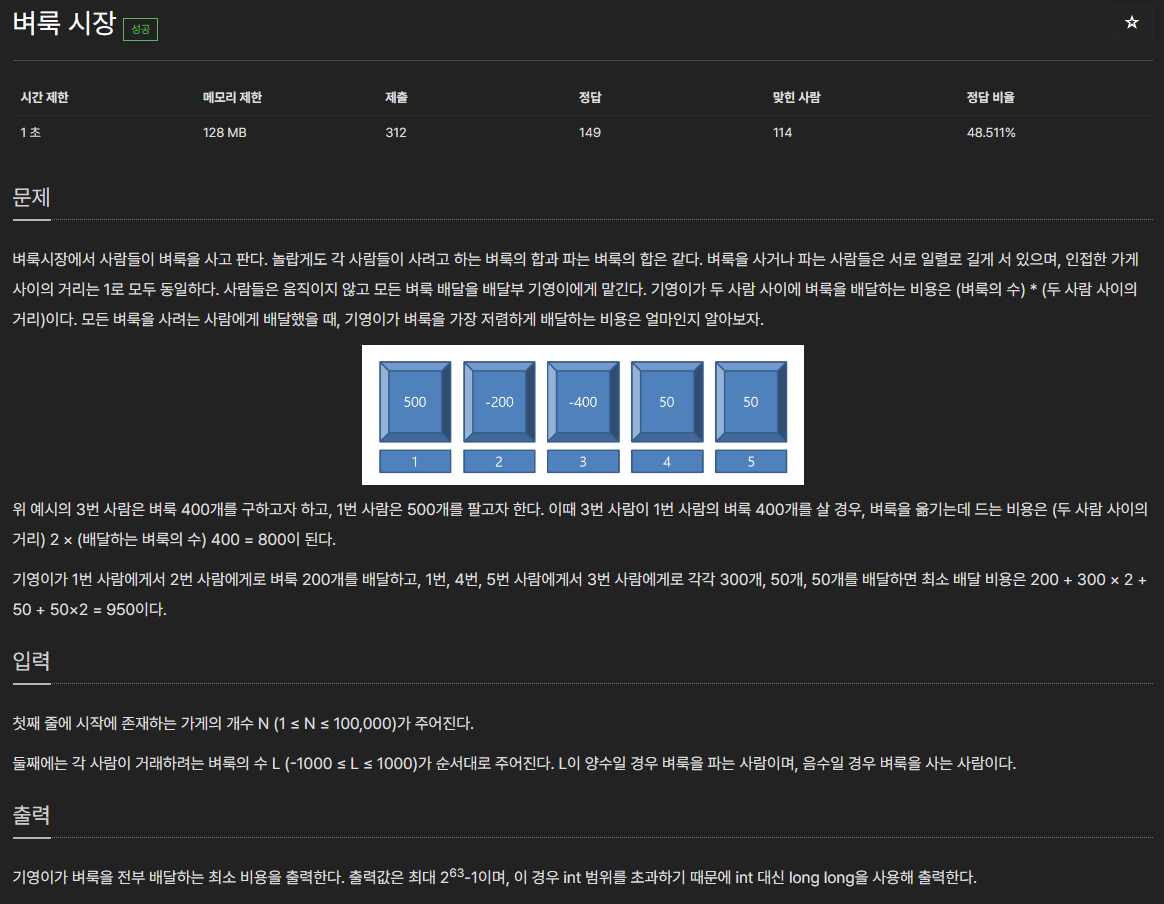
벼룩시장에서 사람들이 벼룩을 사고 판다. 놀랍게도 각 사람들이 사려고 하는 벼룩의 합과 파는 벼룩의 합은 같다. 벼룩을 사거나 파는 사람들은 서로 일렬로 길게 서 있으며, 인접한 가게 사이
www.acmicpc.net
문제 해설
각 사람들이 사려고 하는 벼룩의 합과 파는 벼룩의 합이 같다는 점이 문제 풀이에 큰 도움이 된다. 벼룩을 가장 저렴하게 배달하려면 결국 가장 가까운 사람들에게 벼룩을 배달해야 한다.
문제에서 양수는 벼룩을 파는 사람, 음수는 벼룩을 사는 사람이라는 조건이 있다. 사려고 하는 벼룩의 합이 파는 벼룩의 합과 같고, 벼룩을 가장 저렴하게 배달하려면 가장 가까운 사람에게 배달해야 하기 때문에 시작점에서 출발하여 각 지점의 모든 벼룩을 배달할 벼룩에 추가하고, 다음칸으로 이동할 때마다 현재 벼룩의 수를 배달 비용에 추가할 수 있다.
이 때 벼룩의 개수가 음수인 경우(벼룩을 사는 경우)에는 현재 벼룩의 수가 사려는 벼룩의 수보다 많을 경우에는 그냥 계산하면 되고, 현재 벼룩의 수가 더 적은 경우에는 미리 외상으로 벼룩을 제공하고 이동하면서 음수가 되어 모자란 벼룩을 보충한다는 느낌으로 해결할 수 있다. 이로 인해 현재 벼룩의 수가 음수가 될 수 있기 때문에 배달 비용에 추가할 땐 절대값으로 추가해야 한다. 예제 1의 경우를 보면 다음과 같다.
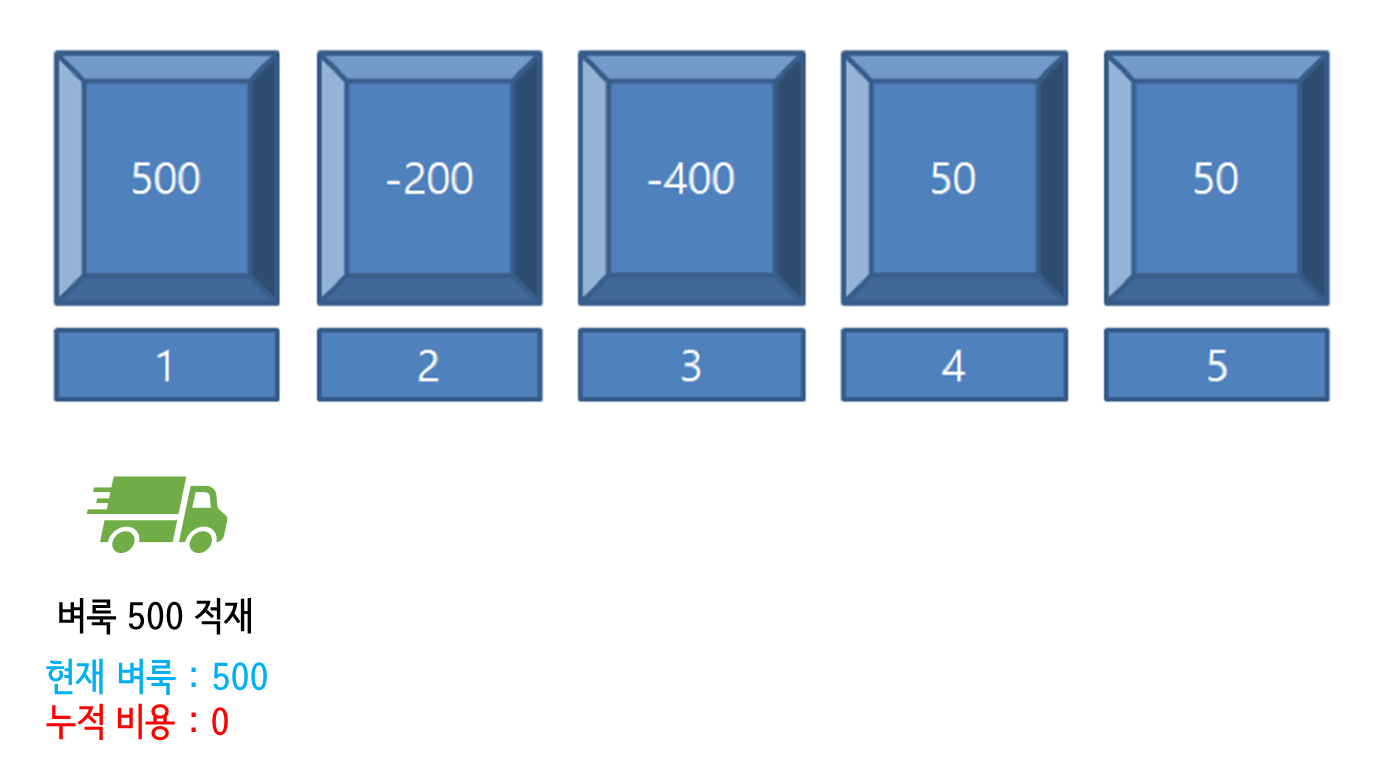
처음 1의 위치에서 벼룩 500마리를 적재한다. 아직 배달을 하지 않았기 때문에 누적 비용은 0이다.
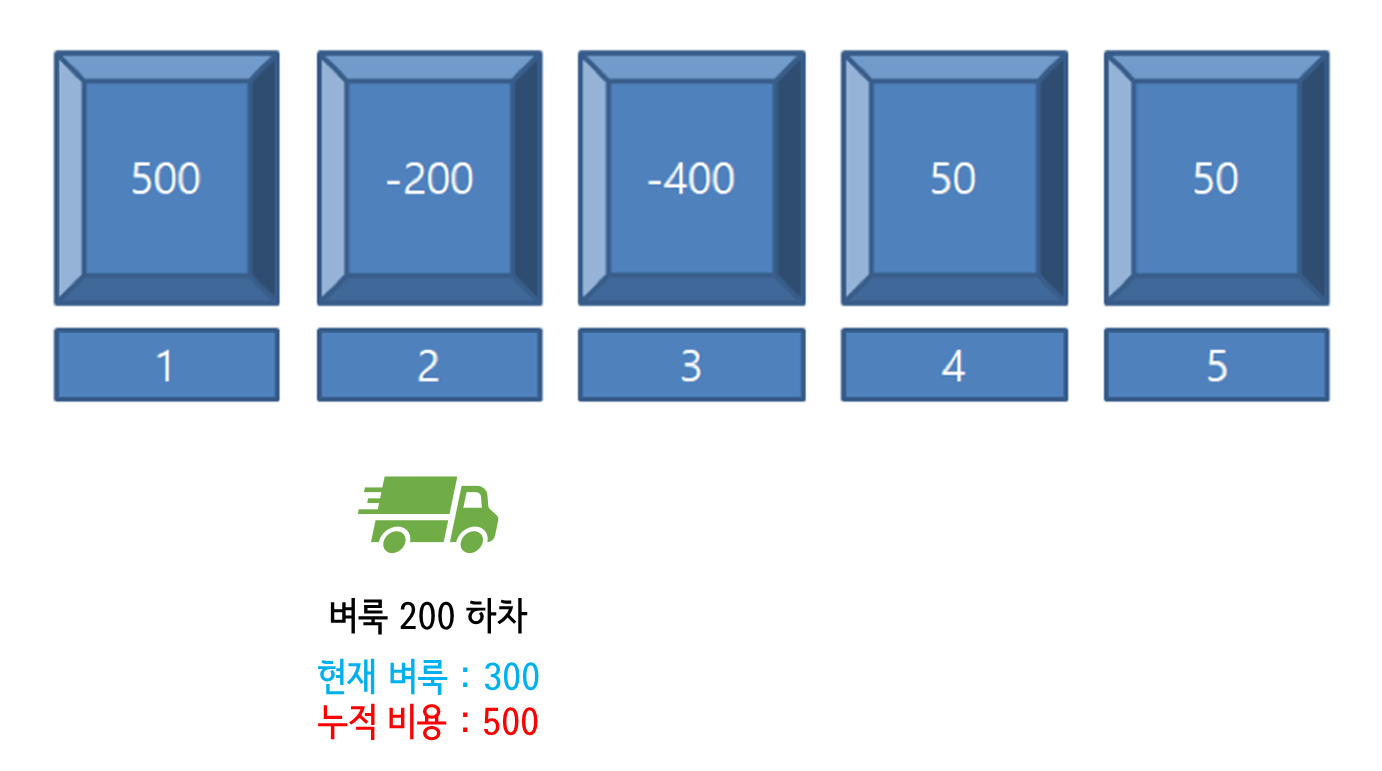
2번 위치에서 벼룩 200마리를 하차한다. 하지만 1번 위치에서 벼룩 500마리를 옮겼기 때문에 누적 비용은 500이 된다.
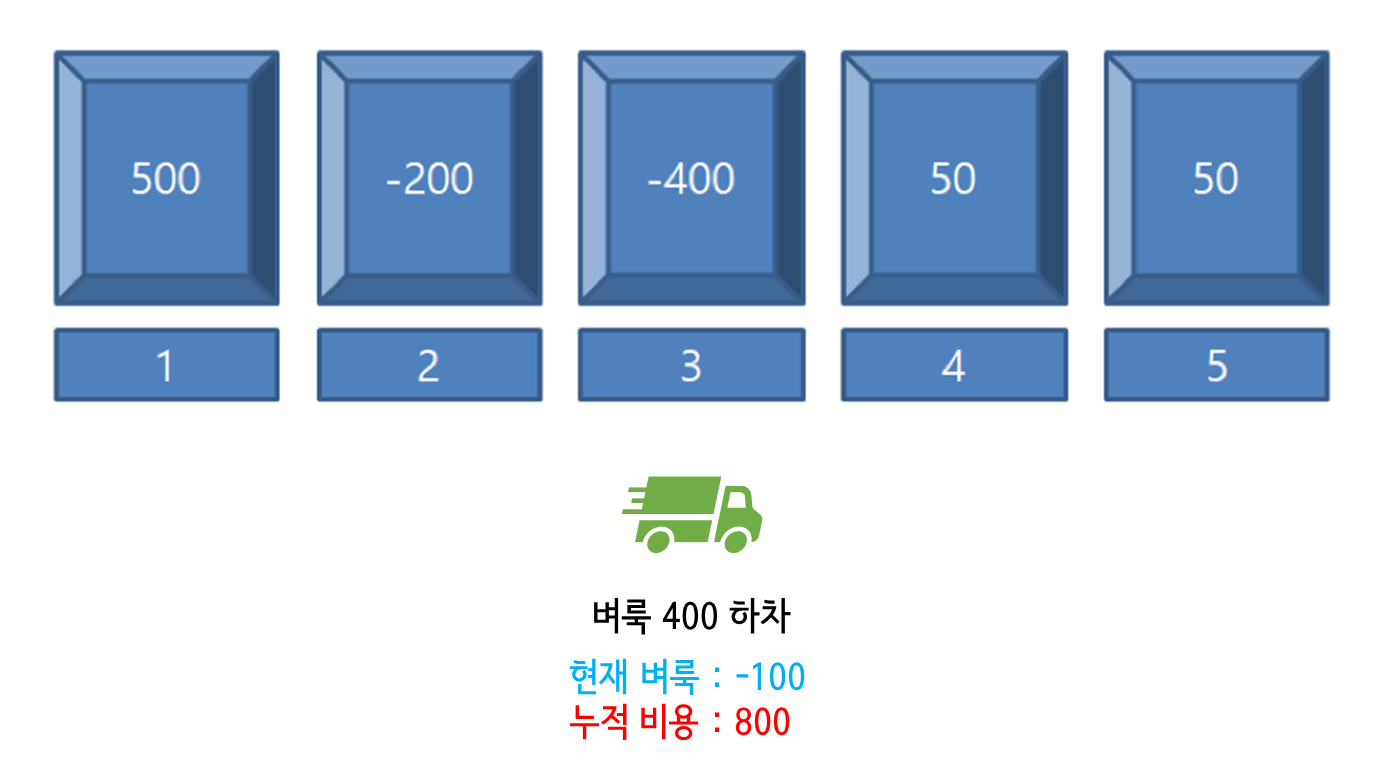
3번 위치에서 벼룩 400마리를 하차한다. 현재 벼룩의 수가 하차할 수보다 적기 때문에 100은 미리 가져다 썼다는 느낌으로 음수로 저장한다. 2번 위치에서 벼룩 300마리를 옮겼기 때문에 누적 비용은 800이 된다.
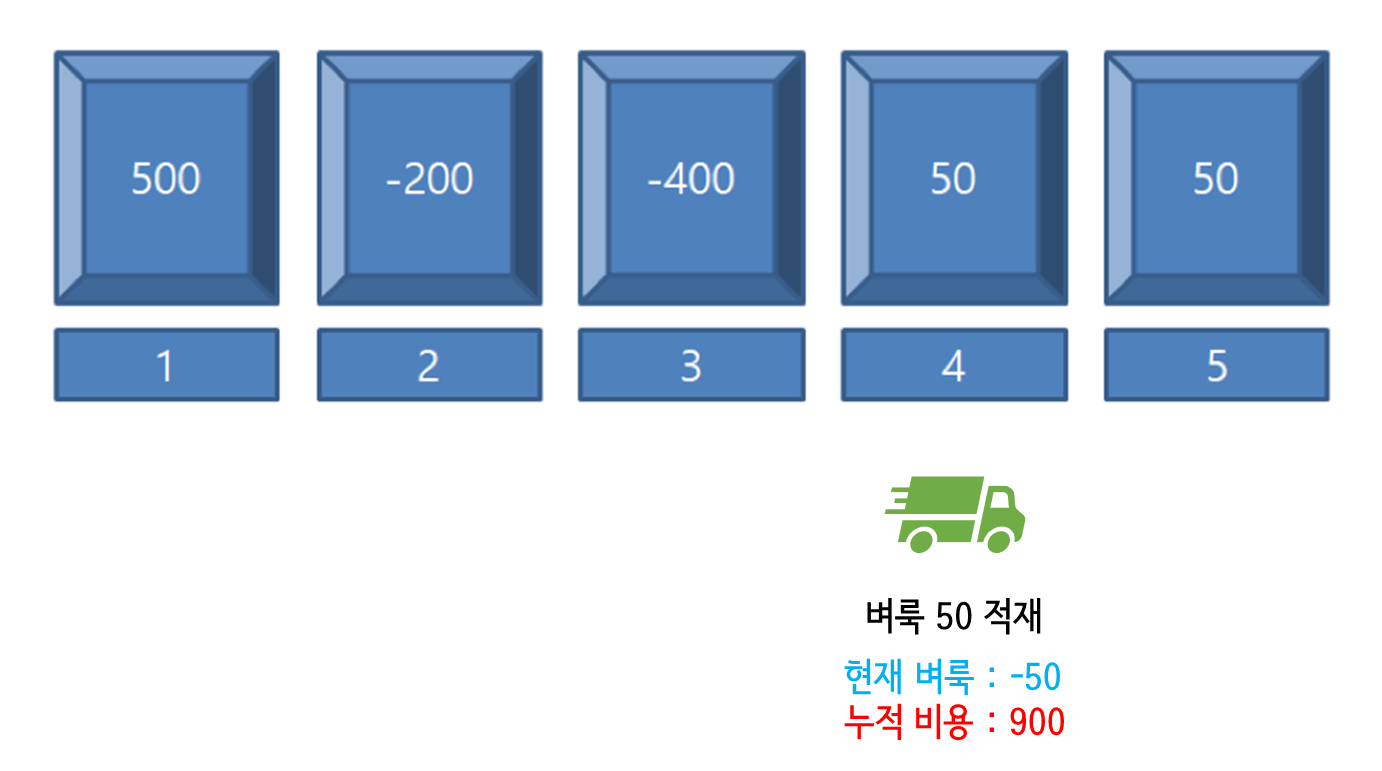
4번 위치에서 벼룩 50마리를 적재한다. 이로 인해 미리 가져다 쓴 100마리 중 50마리를 보충하여 현재 벼룩의 수는 -50이 된다. 3번 위치에서 미리 벼룩 100마리를 옮겼기 때문에 누적 비용은 900이 된다.

5번 위치에서 벼룩 50마리를 적재한다. 모든 배달이 종료되었고, 4번 위치에서 미리 벼룩 50마리를 옮겼기 때문에 누적 비용은 950이 된다.
Code
import java.util.StringTokenizer
import kotlin.math.abs
fun main() = with(System.`in`.bufferedReader()) {
val n = readLine().toInt()
val arr = StringTokenizer(readLine()).run { IntArray(n) { nextToken().toInt() } }
var fleas = 0L
var cost = 0L
for (flea in arr) {
fleas += flea
cost += abs(fleas)
}
println(cost)
}