[Kotlin] 백준 21944 : 문제 추천 시스템 Version 2
문제 링크
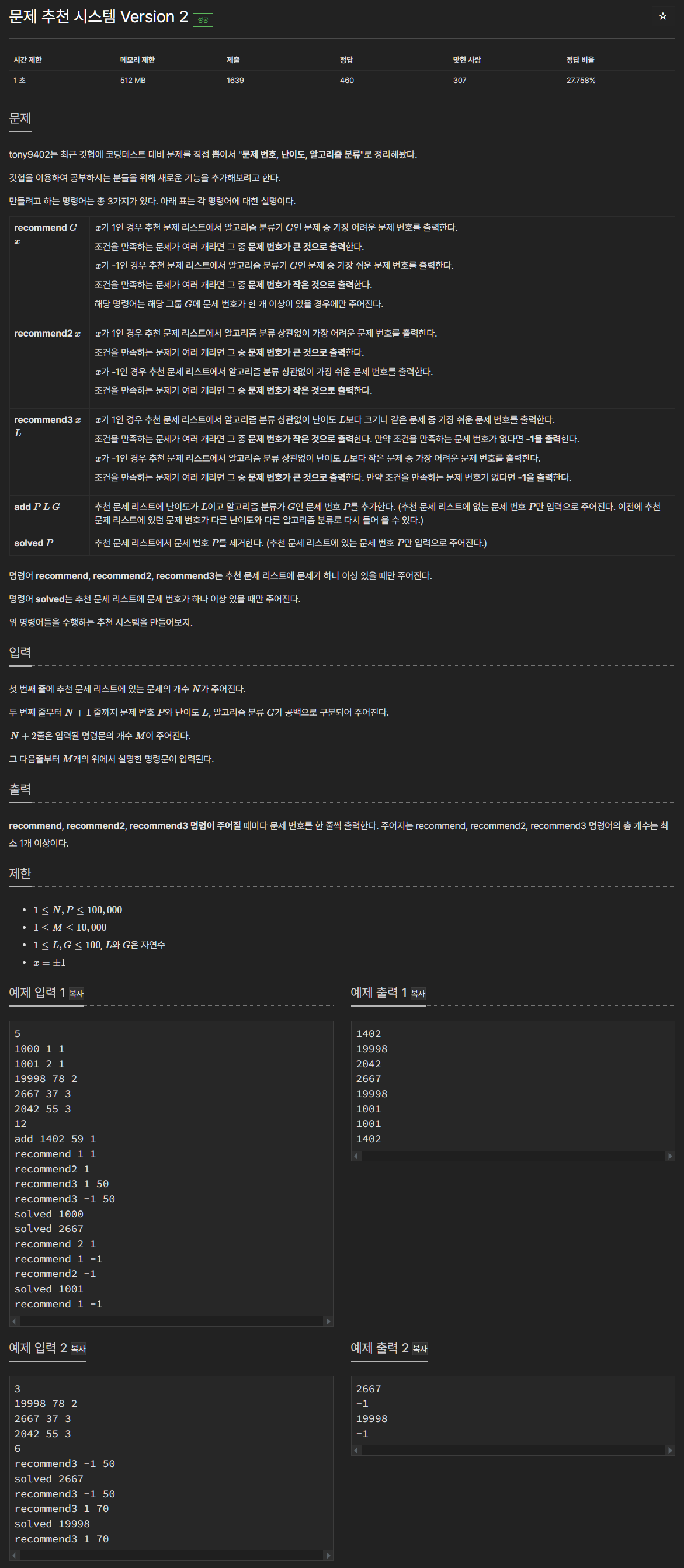
21944번: 문제 추천 시스템 Version 2
recommend, recommend2, recommend3 명령이 주어질 때마다 문제 번호를 한 줄씩 출력한다. 주어지는 recommend, recommend2, recommend3 명령어의 총 개수는 최소 1개 이상이다.
www.acmicpc.net
문제 해설
[Kotlin] 백준 21939 : 문제 추천 시스템 Version 1의 확장 문제. Version 1에서 알고리즘 분류를 비롯하여 추천 명령어 2종류가 추가되었다.
이전 문제와 달리 문제를 객체로 구현하였다. 이 때 문제 클래스는 난이도가 높은 순으로, 난이도가 같다면 문제 번호가 큰 순으로 정렬되도록 Comparable을 구현하여 작성한다.
private class Problem(val number: Int, val difficulty: Int) : Comparable<Problem> {
override fun compareTo(other: Problem) =
if (difficulty == other.difficulty) other.number - number
else other.difficulty - difficulty
override fun toString() = "$number"
}
문제 번호별 난이도와 알고리즘은 동일하게 별도의 정수 배열로 선언한다.
val difficulty = IntArray(100001)
val algorithm = IntArray(100001)
문제는 정렬과 탐색을 빠르게 하기 위해 TreeSet에 담아두는데, 그 외에도 알고리즘 분류별로 문제를 정렬하여 담아 둘 TreeSet 배열도 추가해준다. problemsG의 각 인덱스는 알고리즘 분류 번호를 의미한다.
val problemsG = Array(101) { TreeSet<Problem>() }
val problems = TreeSet<Problem>()
이제 각 명령어에 대한 로직만 구현해주면 된다.
- recommend \(G\) \(x\) : \(x\)가 1이라면
problemsG[G]의 첫번째 문제 번호를, \(x\)가 -1이라면problemsG[G]의 마지막 문제 번호를 출력한다. - recommend2 \(x\) : \(x\)가 1이라면
problems의 첫번째 문제 번호를, \(x\)가 -1이라면problems의 마지막 문제 번호를 출력한다. - recommend3 \(x\) \(L\) : recommend3은 TreeSet의
floor()와ceiling()메소드를 사용한다.floor는 인자로 넘겨준 값 또는 객체보다 작거나 같으면서 가장 큰(우선순위가 높은) 결과를,ceiling()은 인자로 넘겨준 값 또는 객체보다 크거나 같으면서 가장 작은(우선순위가 낮은) 결과를 반환한다. 따라서 \(x\)가 1이라면problems.floor()를, \(x\)가 -1이라면problems.ceiling()를 출력하되, 두 메소드 모두 결과를 찾지 못하면null을 반환하므로 해당 부분을 처리하여 -1을 출력하게 한다. - add \(P\) \(L\) \(G\) :
difficulty의 \(P\) 번째 요소를 \(L\)로,algorithm의 \(P\) 번째 요소를 \(L\)로 변경하고,problemsG[G]와problems에 해당 문제 객체를 추가한다. - solved \(P\) :
problemsG[algorithm[P]]와problems에서 해당 문제 객체를 제거한다.
recommend3에서 탐색하려는 문제 객체의 경우, 난이도가 \(L\)이면서 우선순위가 가장 낮아지도록 인자로 넘겨줄 문제 객체의 번호를 0 이하의 값으로 해야한다. \(x\)가 1이라면 난이도가 \(L\) 이상이어야 하고 \(x\)가 -1이라면 난이도가 \(L\) 미만이어야 하기 때문이다.
Code
import java.util.StringTokenizer
import java.util.TreeSet
fun main() = with(System.`in`.bufferedReader()) {
val bw = System.out.bufferedWriter()
val difficulty = IntArray(100001)
val algorithm = IntArray(100001)
val problemsG = Array(101) { TreeSet<Problem>() }
val problems = TreeSet<Problem>()
fun StringTokenizer.addProblem() {
val (p, l, g) = IntArray(3) { nextToken().toInt() }
val problem = Problem(p, l)
difficulty[p] = l
algorithm[p] = g
problemsG[g].add(problem)
problems.add(problem)
}
repeat(readLine().toInt()) { StringTokenizer(readLine()).addProblem() }
repeat(readLine().toInt()) {
StringTokenizer(readLine()).apply {
when (nextToken()) {
"recommend" -> nextToken().toInt().also {
bw.write(if (nextToken() == "1") "${problemsG[it].first()}\n" else "${problemsG[it].last()}\n")
}
"recommend2" -> bw.write(if (nextToken() == "1") "${problems.first()}\n" else "${problems.last()}\n")
"recommend3" -> {
val x = nextToken()
val problem = Problem(0, nextToken().toInt())
bw.write(if (x == "1") "${problems.floor(problem) ?: -1}\n" else "${problems.ceiling(problem) ?: -1}\n")
}
"add" -> addProblem()
"solved" -> {
val p = nextToken().toInt()
val problem = Problem(p, difficulty[p])
problemsG[algorithm[p]].remove(problem)
problems.remove(problem)
}
}
}
}
bw.close()
}
private class Problem(val number: Int, val difficulty: Int) : Comparable<Problem> {
override fun compareTo(other: Problem) = if (difficulty == other.difficulty) other.number - number else other.difficulty - difficulty
override fun toString() = "$number"
}여담
recommend3을 구현하는 과정에서 좀 애를 먹었다. 처음에는 코틀린에서 모든 컬렉션 타입에 제공하는 firstOrNull()과 lastOrNull()을 사용해보려고 했는데 두 메소드 모두 내부에서 for문으로 구현되어 있는 탓에 시간 초과가 발생했는데 TreeSet의 기본 메소드에 답이 있었다.