[Kotlin] 백준 1850 : 최대공약수
문제 링크
1850번: 최대공약수
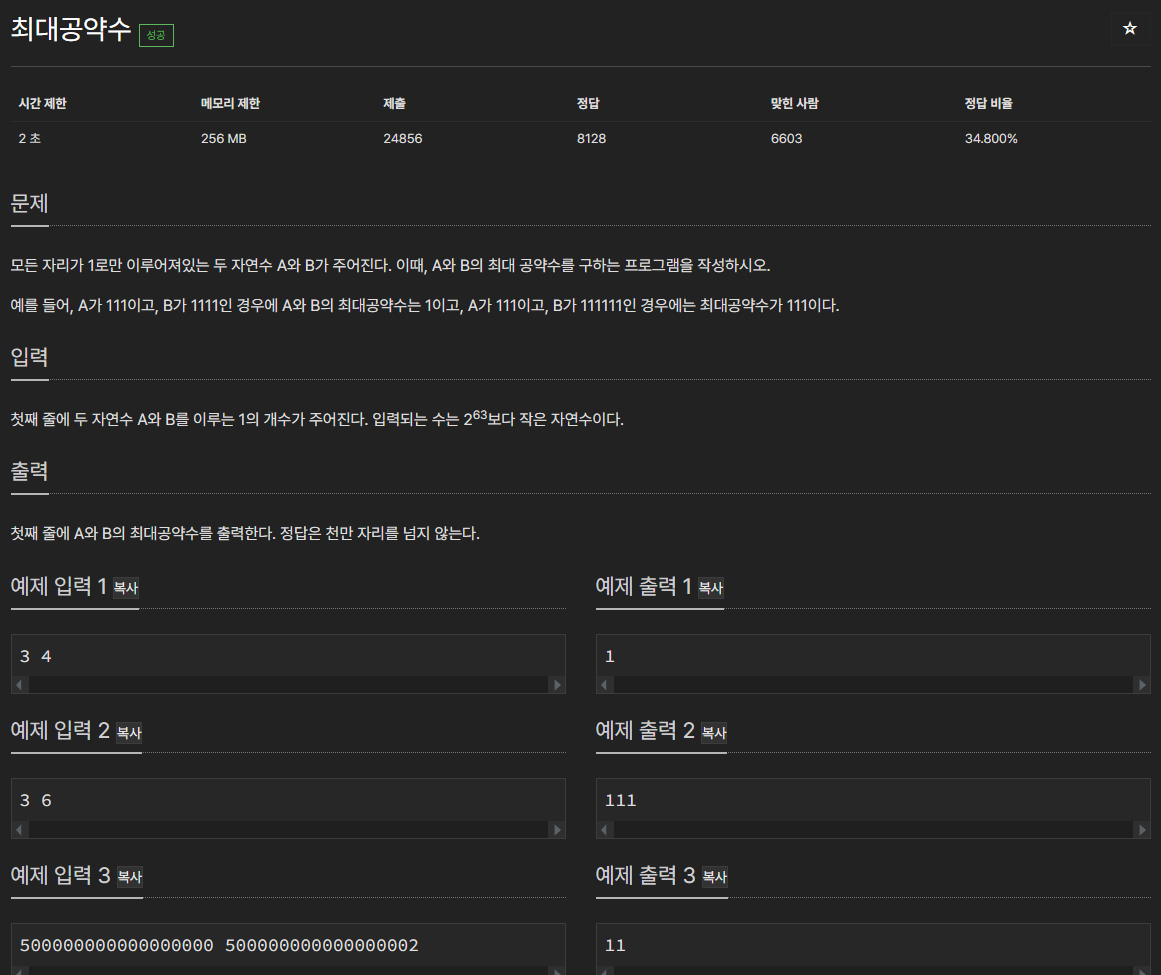
모든 자리가 1로만 이루어져있는 두 자연수 A와 B가 주어진다. 이때, A와 B의 최대 공약수를 구하는 프로그램을 작성하시오. 예를 들어, A가 111이고, B가 1111인 경우에 A와 B의 최대공약수는 1이고, A
www.acmicpc.net
문제 해설
모든 자리가 1로 이루어진 두 수의 최대 공약수를 구해야 한다.
우선 모든 자리가 1로 이루어진 수가 어떻게 구성되는지 보자. \(1111\)의 경우에는 다음과 같이 나눌 수 있다.
$$1111=11\times 101$$
또 다른 수인 \(111111\)은 다음과 같이 나눌 수 있다.
$$\begin{align*}111111&=11\times 10101\\&=111\times 1001\end{align*}$$
자세히 보면 모든 자리가 1로 이루어진 수를 적절히 나누면 모든 자리가 1로 이루어진 어떤 수와 다른 수의 곱으로 나타낼 수 있다는 것을 알 수 있다.
\(1111\)의 자리수는 4고, \(111111\)의 자리수는 6이다. 그리고 4와 6의 최대 공약수는 2이다. 여기서 \(1111\)과 \(111111\)의 최대 공약수는 \(11\)이 되고, 이는 1로만 이루어진 2자리 수(4와 6의 최대 공약수)라는 것을 알 수 있다.
즉, 이 문제에서는 A와 B의 최대공약수를 구해서 그 횟수만큼 1을 출력하면 된다.
주의할 점은 정답이 최대 1000만 자리이기 때문에 Long 타입으로도 표현할 수 없다. 별도의 계산이 필요한 것이 아니라 그저 1을 \(n\)번 반복하여 출력하면 되기 때문에 String 타입으로 출력해주면 된다.
Code
fun main() = with(System.`in`.bufferedReader()) {
val (a, b) = readLine().split(' ').map { it.toLong() }
val gcd = gcd(a, b)
println("1".repeat(gcd.toInt())) // 정답이 최대 1000만자리이기 때문에 Int로 변환해도 된다.
}
private fun gcd(a: Long, b: Long): Long = if (b == 0L) a else gcd(b, a % b)