누적합(Prefix Sum)
일반적으로 배열의 \(n\)번째 인덱스까지의 합을 구할 땐 아래와 같이 반복문을 사용하여 계산하게 된다.
fun sumOfArray(arr: IntArray, n: Int): Int {
var sum = 0
for (i in 0..n) {
sum += arr[i]
}
return sum
}이 경우는 합을 한 번만 구할 때는 문제없이 사용할 수 있으나, \(N=[n_{1}, n_{2}, n_{3}, \cdots, n_m]\)와 같은 \(m\) 개의 경우에 대해 각 \(n\)번째 인덱스까지의 합을 구하는 경우엔 \(n\)만큼의 연산을 \(m\) 번 반복하게 된다. 즉, 총 시간 복잡도는 \(O(nm)\)이 된다.
누적합은 배열의 요소가 변하지 않는다는 점을 이용한다. 원본 배열의 요소가 변하지 않기 때문에 어떠한 \(n\)번째 인덱스까지의 합도 변하지 않는다. 그러면 \(S[n] = A[0] + A[1] + A[2] + \cdots + A[n-1] + A[n]\)이 된다. 여기서 \(S[n - 1] = A[0] + A[1] + A[2] + \cdots + A[n-1]\)이므로 \(S[n] = S[n-1] + A[n]\)이라는 결론이 도출된다. 이과정을 그림과 코드로 나타내면 다음과 같다.
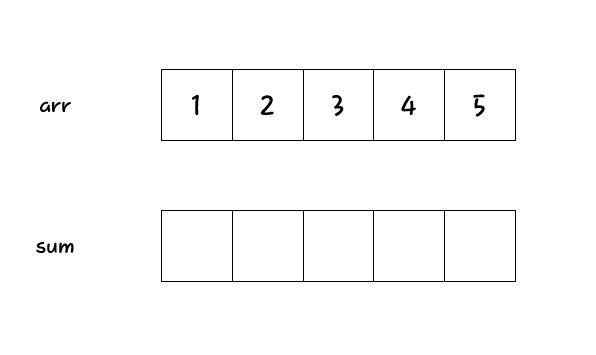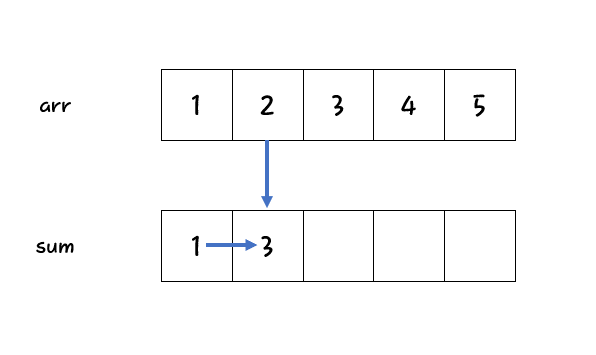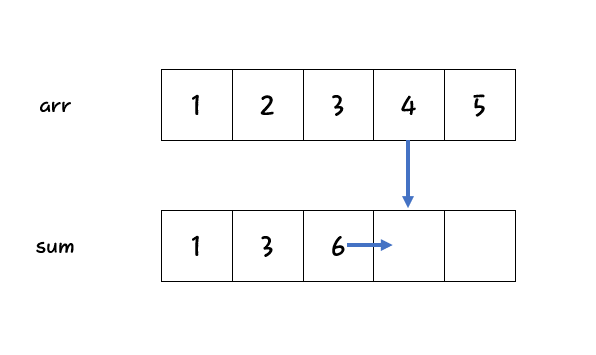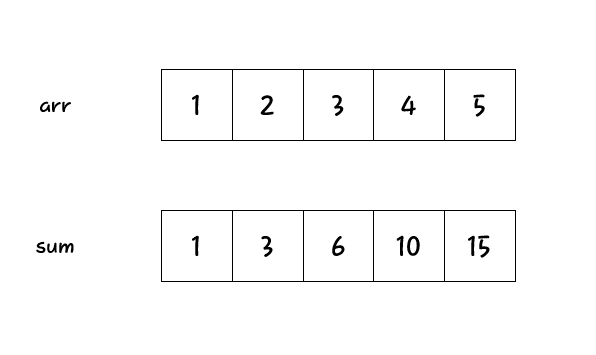
fun prefixSum(arr: IntArray): IntArray {
val result = IntArray(arr.size)
for (i in 1..arr.lastIndex) {
result[i] = result[i - 1] + arr[i]
}
return result
}첫 번째의 합을 구하는 코드와는 별도의 배열을 생성하여 \(i\)번째 인덱스까지의 합을 각 인덱스에 저장하여 반환한다는 차이점이 있다. 이렇게 크기가 \(n\)인 배열 전체에 대해서 누적합을 저장해두면 \(i\)번째 인덱스까지의 합을 구할 땐 누적합이 저장된 배열의 \(i\)번째 값만 가져오면 되므로 \(m\) 개의 경우에 대한 총 시간 복잡도는 \(O(n+m)\)이 된다.
여기서 1번 인덱스부터 시작한 이유는 누적합을 구할 때 \(n-1\)번째 인덱스를 이용해야 하는데, 0번 인덱스부터 시작하면 \(0-1=-1\)이 되어 ArrayIndexOutOfBoundsException이 발생하기 때문에 그에 대한 처리를 해야 해서 번거로워지기 때문이다. 당연히 파라미터로 받게 되는 원본 배열도 0번째 값은 비워둬야 한다.
부분합(Partial Sum)
배열의 \(i\)번째 요소부터 \(j\)번째 요소까지의 합을 구하는 부분합도 일반적으로는 단순 반복문으로 구하는 경우가 많다.
fun partialSum(arr: IntArray, n: Int, m: Int): Int {
var sum = 0
for (i in n..m) {
sum += arr[i]
}
return sum
}이 경우도 \(m\)개의 경우에 대해 같은 방법을 사용하게 되면 총 시간 복잡도가 \(O(nm)\)이 된다. 하지만 위에서 구한 누적합을 이용하면 \(m\)개의 경우에 대한 부분합도 \(O(n+m\)의 시간 복잡도로 구할 수 있다.
\(i\leq j\)일 때 \(A[i]\)부터 \(A[j]\)까지의 모든 요소의 합은 위의 누적합을 이용하였을 때 \(S[j] - S[i - 1]\)이 된다. \(i\leq j\)이기 때문에 \(S[j] = A[1]+A[2]+A[3]+\cdots +A[i-1]+A[i]+A[i+1]+\cdots +A[j-1]+A[j]\)가 된다. 여기서 \(A[1]+A[2]+A[3]+\cdots +A[i-1]+A[i] = S[i - 1]\)이기 때문에 \(S[j]=S[i-1]+A[i]+A[i+1]+\cdots +A[j-1]+A[j]\)가 되고 \(A[i]\)부터 \(A[j]\)까지 모든 요소의 합을 \(S[i..j]\)라고 하면 \(S[j]=S[i-1]+S[i..j]\)이기 때문에 \(S[i..j]=S[j]-S[i-1]\)이 성립하게 된다. 따라서 위의 누적합을 저장한 배열을 이용하면 부분합을 구하는 코드를 아래와 같이 바꿀 수 있다.
fun partialSum(prefixSum: IntArray, n: Int, m: Int): Int {
return prefixSum[m] - prefixSum[n - 1]
}여기서도 누적합 배열은 0번 인덱스를 비워두고 1번 인덱스부터 시작한다. 여기서 partialSum()이 받는 파라미터인 prefixSum은 누적합을 저장해둔 배열이고, \(n\leq m<\) prefixSum.size이다. 이 또한 누적합을 한 번만 구해놓으면 누적합 배열에서 요소 2개를 뽑아와서 계산만 하면 되므로 각 경우의 시간 복잡도는 \(O(2)=O(1)\)이 되고, 총 시간 복잡도는 \(O(n+2m)=O(n+m)\)이 되어 매 경우마다 계산할 때보다 효율적으로 부분합을 구할 수 있다.
'Algorithm > 관련내용' 카테고리의 다른 글
| [Kotlin] 코틀린으로 정렬 관련 문제를 풀 때 사용하는 배열이나 리스트를 정렬하는 메소드의 종류 및 각 메소드의 차이 (2) | 2023.03.31 |
|---|---|
| [Kotlin] 코틀린으로 알고리즘 문제를 풀 때 출력 방식별 속도에 대하여 (0) | 2023.01.20 |
| 투 포인터(Two Pointer) with Kotlin (0) | 2022.12.18 |
| [Kotlin/Java] 소수 찾기와 에라토스테네스의 체 (0) | 2022.11.29 |





댓글