문제 링크
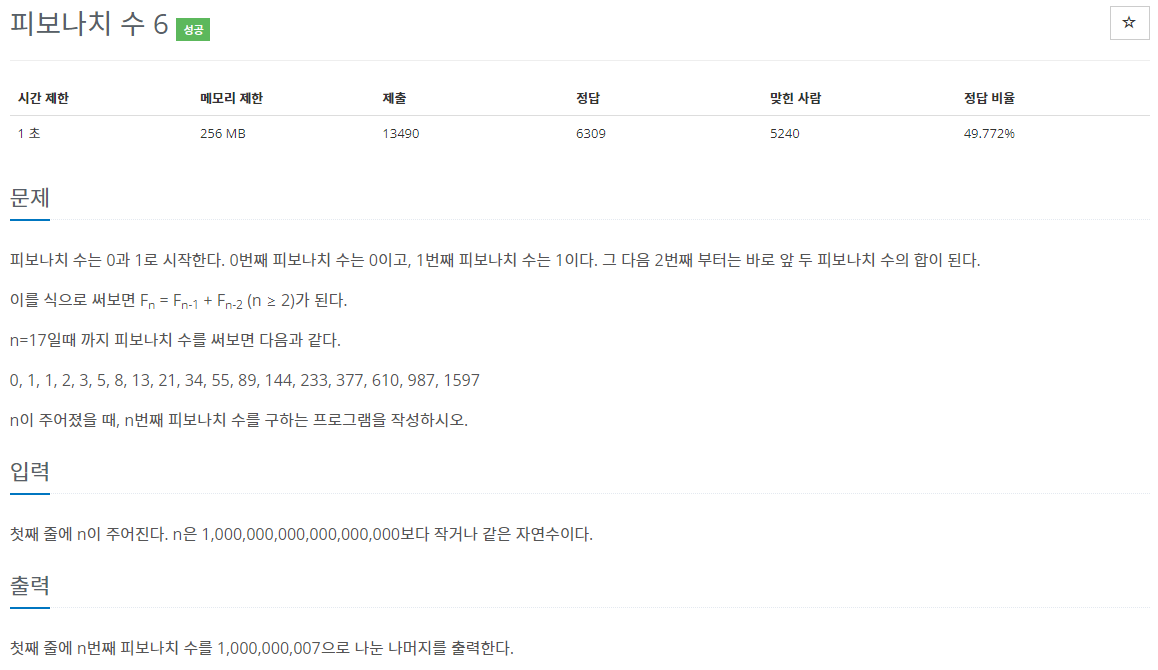
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
문제 해설
피보나치 수를 구하는 문제지만 입력이 굉장히 큰 경우다. 이 경우 피보나치 수를 구하는 일반적인 식인 \(F_n=F_{n-1}+F_{n-2}\)을 사용하게 되면 최대 \(10^{18}\)번의 연산을 수행해야 하기 때문에 이 방법은 사용할 수 없다.
문제를 해결하기 위해서는 더 효율적인 방법을 찾아야 하는데, 피보나치 수를 구하는 방법 중에는 도가뉴 항등식(d'Ocagne's identity)이라는 것이 있다. 도가뉴 항등식의 형태는 다음과 같다.
$$F_{m+n}=F_{m-1}F_n+F_mF_{n+1}$$
여기서 \(m\)에 \(n\)을 대입하면 다음과 같은 식을 얻을 수 있다.
$$\begin{align*}F_{2n}&=F_{n-1}F_n+F_nF_{n+1}\\&=F_n(F_{n-1}+F_{n+1})\\&=F_n(F_{n-1}+F_{n-1}+F_n)\\&=F_n(2F_{n-1}+F_n)\end{align*}$$
이 경우는 입력이 짝수인 경우에만 사용할 수 있으므로 홀수인 경우에 사용할 식도 있어야 한다. 따라서 \(m\)에 \(n+1\)을 대입하면 다음과 같은 식을 얻을 수 있다.
$$\begin{align*}F_{2n+1}&=F_nF_n+F_{n+1}F_{n+1}\\&=F_n^2+F_{n+1}^2\end{align*}$$
이제 \(O(\log{n})\)의 시간 복잡도로 피보나치 수를 구할 수 있는 새로운 공식을 얻게 되었다. 이미 구한 피보나치 수의 중복 계산을 방지하기 위해 피보나치 수를 저장할 Map을 만들어 피보나치 수를 저장하고, 위에서 얻은 식을 이용하여 재귀 함수를 작성하면 문제를 해결할 수 있다.
Code
import java.math.BigInteger
fun main() = with(System.`in`.bufferedReader()) {
println(fibonacci(readLine().toBigInteger()))
}
private val B0 = 0.toBigInteger()
private val B1 = 1.toBigInteger()
private val B2 = 2.toBigInteger()
private val fibonacciMemory = HashMap<BigInteger, Long>().apply {
put(B0, 0L)
put(B1, 1L)
}
private fun fibonacci(n: BigInteger): Long {
if (fibonacciMemory[n] == null) {
val f_n = fibonacci(n / B2)
when (n % B2) {
B0 -> fibonacciMemory[n] = (f_n * (2 * fibonacci(n / B2 - B1) + f_n)) % 1000000007
B1 -> fibonacciMemory[n] = (f_n * f_n + fibonacci(n / B2 + B1) * fibonacci(n / B2 + B1)) % 1000000007
}
}
return fibonacciMemory[n] ?: 0L
}'Algorithm > BOJ' 카테고리의 다른 글
| [Kotlin] 백준 23300 : 웹 브라우저 2 (0) | 2023.01.26 |
|---|---|
| [Kotlin] 백준 26597 : 이 사람 왜 이렇게 1122를 좋아함? (0) | 2023.01.25 |
| [Kotlin] 백준 23309 : 철도 공사 (0) | 2023.01.19 |
| [Kotlin] 백준 1283 : 단축키 지정 (1) | 2023.01.18 |
| [Kotlin] 백준 23629 : 이 얼마나 끔찍하고 무시무시한 수식이니 (0) | 2023.01.14 |





댓글