문제 링크
6568번: 귀도 반 로썸은 크리스마스날 심심하다고 파이썬을 만들었다
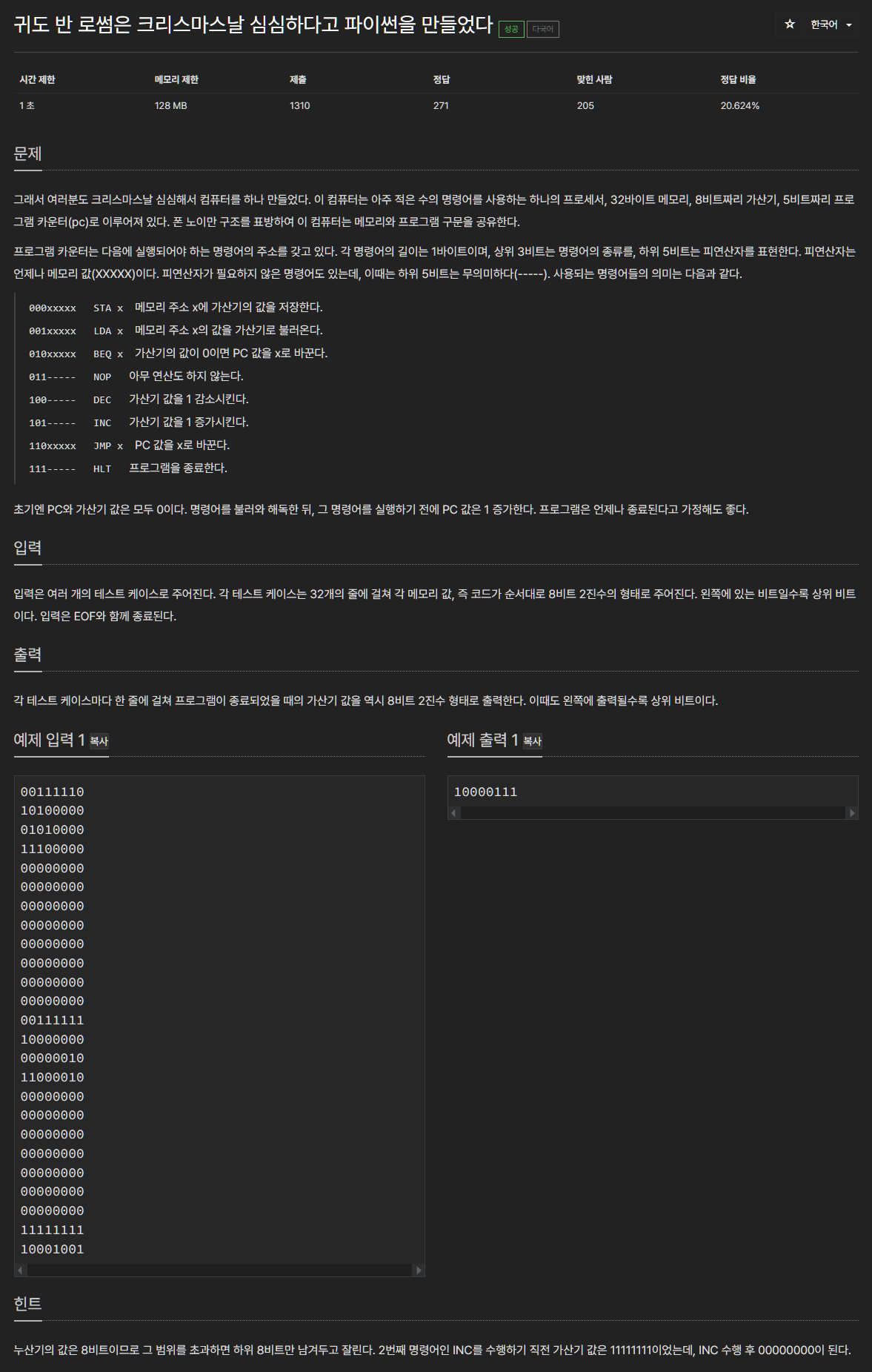
그래서 여러분도 크리스마스날 심심해서 컴퓨터를 하나 만들었다. 이 컴퓨터는 아주 적은 수의 명령어를 사용하는 하나의 프로세서, 32바이트 메모리, 8비트짜리 가산기, 5비트짜리 프로그램 카
www.acmicpc.net
문제 해설
특별한 알고리즘이 필요하진 않은 아닌 단순 구현 문제. 뭔가 복잡해보이지만 차근차근 문제에서 요구하는 내용을 구현해보자.
먼저 컴퓨터의 메모리가 32바이트라고 되어있다. 또한 이 컴퓨터는 메모리와 프로그램 구문(명령어)를 공유한다는 조건이 있고, 각 명령어의 길이가 1바이트라는 언급이 있으므로 길이가 32인 정수 배열로 나타낼 수 있다.
각 명령어는 3비트의 명령어 종류와 5비트의 피연산자를 표현한다고 되어있다. 즉 각 명령어는 2진수로 표현된 8비트의 정수라는 것과 명령어 종류는 명령어를 \(2^5=32\)로 나눈 몫, 피연산자는 명령어를 (2^5=32\)로 나눈 나머지라는 것을 알 수 있다.
이제 프로그램 카운터(PC)와 가산기, 메모리에 저장된 명령어를 통해 구현만 해주면 된다. 이 때 가산기의 용량은 8비트이기 때문에 \(0\)부터 \(2^8-1=255\)까지, PC의 용량은 5비트이기 때문에 \(0\)부터 \(2^5-1=31\)까지만 저장할 수 있다. 따라서 가산기에 저장된 값이 증가 또는 감소할 때는 \(256\)으로, PC의 값이 증가할 때는 \(32\)로 모듈러 연산을 수행해야 한다.
뺄셈은 조금 생각해볼게 있는데 위에서 가산기에 저장된 값의 범위를 0~255로 지정했다. 단순히 뺄셈을 수행하면 음수값이 나와서 계산하기 번거로워지는데 이는 컴퓨터에서 뺄셈을 수행하는 방식의 특징을 이용할 수 있다.
컴퓨터에서는 뺄셈을 수행할 때 음수의 덧셈, 즉 2의 보수의 덧셈을 수행하게 된다. 8비트 크기의 정수에서 \(1\)을 빼면 \(1\)의 2의 보수인 \(11111111\)을 더하는 것과 같다. 이를 부호 없는 10진수로 변환하면 \(255\)를 더하는것과 같으므로 \(255\)를 더하고 256으로 모듈러 연산을 수행하면 된다.
문제가 여러 테스트 케이스를 EOF까지 받는 문제이기 때문에 첫 입력이 null인지 확인하는 조건으로 반복해서 수행해야 한다.(코드에서는 로컬에서의 테스트를 위해 isNullOrEmpty() 메소드를 사용했다.)
Code
fun main() = with(System.`in`.bufferedReader()) {
val bw = System.out.bufferedWriter()
var firstInput: String?
while (!readLine().also { firstInput = it }.isNullOrEmpty()) {
val memory = intArrayOf(firstInput!!.toInt(2)) + IntArray(31) { readLine().toInt(2) }
var pc = 0
var adder = 0
while (true) {
val opperator = memory[pc] / 32
val operand = memory[pc++] % 32
pc %= 32
when (opperator) {
0 -> memory[operand] = adder
1 -> adder = memory[operand]
2 -> if (adder == 0) pc = operand
3 -> continue
4 -> adder = (adder + 255) % 256
5 -> adder = (adder + 1) % 256
6 -> pc = operand
7 -> break
}
}
bw.write("${adder.toString(2).padStart(8, '0')}\n")
}
bw.close()
}'Algorithm > BOJ' 카테고리의 다른 글
| [Kotlin] 백준 21944 : 문제 추천 시스템 Version 2 (0) | 2023.09.13 |
|---|---|
| [Kotlin] 백준 27162 : Yacht Dice (0) | 2023.09.05 |
| [Kotlin] 백준 20551 : Sort 마스터 배지훈의 후계자 (0) | 2023.08.23 |
| [Kotlin] 백준 1644 : 소수의 연속합 (0) | 2023.08.11 |
| [Kotlin] 백준 12789 : 도키도키 간식드리미 (0) | 2023.08.09 |





댓글