문제 링크
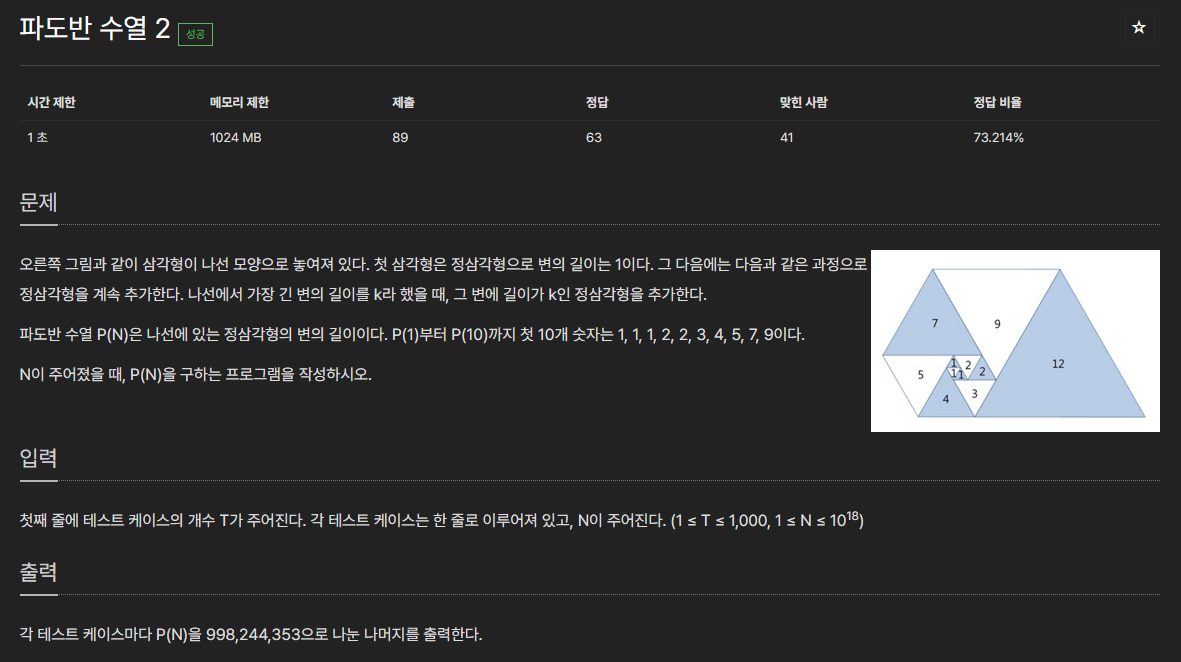
27435번: 파도반 수열 2
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ T ≤ 1,000, 1 ≤ N ≤ 1018)
www.acmicpc.net
문제 해설
[Kotlin] 백준 9461 : 파도반 수열의 확장 버전 문제이다. 이전 문제는 입력값이 최대 100이었기 때문에 DP로 충분히 해결할 수 있는 문제였지만, 이 문제는 입력값이 최대 1018이나 되기 때문에 DP로 풀게 되면 시간초과가 발생한다. 따라서 파도반 수열의 성질을 이용하여 풀어야 한다.
파도반 수열에 대해 다음과 같이 피보나치 Q-행렬과 유사한 행렬(이하 Q-행렬)이 존재한다.
$$Q=\begin{bmatrix}0&1&0\\0&0&1\\1&1&0\\\end{bmatrix}$$
그리고 어떤 수 \(n\)의 파도반 수열 \(P(n)\)에 대하여 Q-행렬의 거듭 제곱이 다음과 같은 형태로 나타나게 된다.
$$Q^n=\begin{bmatrix}P(n-4)&P(n-2)&P(n-3)\\P(n-3)&P(n-1)&P(n-2)\\P(n-2)&P(n)&P(n-1)\\\end{bmatrix}$$
이를 잘 활용하면 \(O(\log n)\)의 시간 내에 \(P(n)\)을 구할 수 있다.
먼저 \(3\times 3\) 크기의 단위행렬과 파도반 Q-행렬을 선언한다. 그 후 \(n=0\)이 될 때까지 \(n\)을 반으로 줄여나가면서 Q-행렬을 제곱해나간다.
그런데 \(n\)이 홀수인 경우도 고려를 해야한다. \(n\)이 홀수일 때는 먼저 선언해둔 단위행렬에 지금까지 계산해둔 Q-행렬의 거듭제곱을 곱해준다. 이 모든 과정을 코드로 나타내면 다음과 같다.
while (n >= 1) {
if (n % 2 == 1L) {
base *= q_matrix
}
q_matrix *= q_matrix
n /= 2
}예를 들어 \(n=100\)일 때 위의 계산을 진행해보면 다음과 같아진다.
$$\begin{align*}\\&n=100,\quad E=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix},\quad Q=\begin{bmatrix}0&1&0\\0&0&1\\1&1&0\\\end{bmatrix}\qquad\cdots (1)\\&n=50,\quad E=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix},\quad Q=Q^2\qquad\cdots (2)\\&n=25,\quad E=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}\quad, Q=(Q^2)^2=Q^4\qquad\cdots (3)\\&n=12,\quad E=Q^4,\quad Q=(Q^4)^2=Q^8\qquad\cdots (4)\\&n=6,\quad E=Q^4,\quad Q=(Q^8)^2=Q^{16}\qquad\cdots (5)\\&n=3,\quad E=Q^4,\quad Q=(Q^{16})^2=Q^{32}\qquad\cdots (6)\\&n=1,\quad E=Q^4\times Q^{32}=Q^{36},\quad Q=(Q^{32})^2=Q^{64}\qquad\cdots (7)\\&n=0,\quad E=Q^{36}\times Q^{64}=Q^{100},\quad Q=(Q^{64})^2=Q^{128}\qquad\cdots (8) && \end{align*}$$
여기서 \(Q^{100}\)의 내용은 다음과 같다.
$$Q^{100}=\begin{bmatrix}P(96)&P(98)&P(97)\\P(97)&P(99)&P(98)\\P(98)&P(100)&P(99)\end{bmatrix}$$
따라서, 어떤 수 \(n\)에 대한 \(P(n)\)의 값은 모든 계산을 수행한 base의 2행, 1열 값이 된다.
행렬곱을 사용한 방법보다 비효율적이긴 하지만, 행렬곱을 사용하지 않고 [Kotlin] 백준 11444 : 피보나치 수 6에서 사용한 도가뉴 항등식과 유사하게 재귀적으로 푸는 방법도 있다. 위의 Q-행렬에서 \(n\)에 \(2n+1\)을 대입하면 다음 식을 얻을 수 있다.
$$\begin{align*}Q^{2n+1}&=\begin{bmatrix}P(n-4)&P(n-2)&P(n-3)\\P(n-3)&P(n-1)&P(n-2)\\P(n-2)&P(n)&P(n-1)\end{bmatrix}\begin{bmatrix}P(n-3)&P(n-1)&P(n-2)\\P(n-2)&P(n)&P(n-1)\\P(n-1)&P(n+1)&P(n)\end{bmatrix}\\&=\begin{bmatrix}P(2n-4)&P(2n-2)&P(2n-3)\\P(2n-3)&P(2n-1)&P(2n-2)\\P(2n-2)&P(2n)&P(2n-1)\end{bmatrix}&&\end{align*}$$
위 식의 행렬곱을 수행하여 정리하면 다음 두 식을 얻을 수 있다.
$$\begin{align*}\\&P(2n)=P(n-2)^2+2P(n-1)P(n)\\&P(2n+1)=P(n-1)(P(n+1)+P(n-2))+P(n)^2&&\end{align*}$$
파도반 수열의 점화식으로 인해 \(P(n+1)=P(n-1)+P(n-2)\)이므로 \(P(2n+1)\)식을 정리하면 다음 식을 얻을 수 있다.
$$P(2n+1)=P(n-1)(P(n-1)+2P(n-2))+P(n)^2$$
새로운 파도반 수열의 관계식을 구했으니 \(P(n)\)을 저장해둘 Map을 선언하여 \(P(-1)=1\), \(P(0)=0\), \(P(1)=1\)만 저장해두고 재귀함수를 호출하면 된다. 음의 파도반 수열 초기값은 파도반 수열 영문위키에서 참고하였다.(해당 문서에서는 파도반 수열이 \(P(0)\)부터 시작하지만, 본 문제는 \(P(1)\)부터 시작한다는 점을 염두해두어야 한다.)
Code : Q-행렬
fun main() = with(System.`in`.bufferedReader()) {
val bw = System.out.bufferedWriter()
repeat(readLine().toInt()) {
var base = arrayOf(longArrayOf(1, 0, 0), longArrayOf(0, 1, 0), longArrayOf(0, 0, 1))
var q_matrix = arrayOf(longArrayOf(0, 1, 0), longArrayOf(0, 0, 1), longArrayOf(1, 1, 0))
var n = readLine().toLong()
if (n <= 3) {
bw.write("1\n")
} else {
while (n >= 1) {
if (n % 2 == 1L) {
base *= q_matrix
}
q_matrix *= q_matrix
n /= 2
}
bw.write("${base[2][1]}\n")
}
}
bw.close()
}
private operator fun Array<LongArray>.times(matrix: Array<LongArray>): Array<LongArray> {
val result = Array(size) { LongArray(matrix[0].size) }
for (i in indices) {
for (j in matrix[0].indices) {
for (k in matrix.indices) {
result[i][j] += this[i][k] * matrix[k][j]
}
result[i][j] = result[i][j] % 998244353
}
}
return result
}Code : 재귀
fun main() = with(System.`in`.bufferedReader()) {
val bw = System.out.bufferedWriter()
repeat(readLine().toInt()) {
bw.write("${padovan(readLine().toLong())}\n")
}
bw.close()
}
private val memory = HashMap<Long, Long>().also {
it[-1] = 1
it[0] = 0
it[1] = 1
}
private fun padovan(n: Long): Long {
return memory[n] ?: run {
val half = n / 2
val p_n = padovan(half)
val p_n_1 = padovan(half - 1)
val p_n_2 = padovan(half - 2)
((if (n % 2 == 0L) p_n_2 * p_n_2 + 2 * p_n_1 * p_n else p_n_1 * (p_n_1 + 2 * p_n_2) + p_n * p_n) % 998244353)
.also { memory[n] = it }
}
}두 코드의 효율 차이

아래의 결과가 Q-행렬을 사용한 코드이고 위의 결과가 재귀식을 사용한 코드이다. Q-행렬을 사용한 코드가 약 2배정도 더 효율적인 것을 볼 수 있다.
재귀식의 경우에는 \(P(n)\)을 구할때마다 추가적인 파도반 수열을 구해야해서 그런게 아닐까 생각한다.
참조 링크
Padovan sequence - Wikipedia
From Wikipedia, the free encyclopedia Sequence of integers In number theory, the Padovan sequence is the sequence of integers P(n) defined[1] by the initial values P ( 0 ) = P ( 1 ) = P ( 2 ) = 1 , {\displaystyle P(0)=P(1)=P(2)=1,} and the recurrence relat
en.wikipedia.org
Wolfram MathWorld: The Web's Most Extensive Mathematics Resource
Comprehensive encyclopedia of mathematics with 13,000 detailed entries. Continually updated, extensively illustrated, and with interactive examples.
mathworld.wolfram.com
'Algorithm > BOJ' 카테고리의 다른 글
| [Kotlin] 백준 14943 : 벼룩 시장 (0) | 2023.05.15 |
|---|---|
| [Kotlin] 백준 1700 : 멀티탭 스케줄링 (0) | 2023.05.04 |
| [Kotlin] 백준 27450 : 플래그 대사 좀 그만 말해요 (0) | 2023.04.23 |
| [Kotlin] 백준 27960 : 사격 내기 (0) | 2023.04.20 |
| [Kotlin] 백준 23294 : 웹 브라우저 1 (0) | 2023.04.19 |





댓글